(1)0909・・・2桁の数字には一致しますが、「1」や「2」には一致しません。 (2)09?09・・・1桁の数字には一致しますが、「00」や「09」にも一致します。 (3)19?09・・・十の位は、「1」から「9」までの数字だけに一致するようにします。 <001から0Q1 に1から9までの数字を入 れて、次の式が成り立つようにしなさい。 10年現在43個の完全数が,コンピュータを使って 自然数の和 一般項が an = n a n = n となる数列 {an} { a n } を考えてみましょう。 これは、 1 1 から順番に数字が並んでいる数列です。 差が一定なので、この数列は等差数列になります。 この数列の、初項から第 n 項までの和を求めてみましょう。 基本等差数列の和 の内容を使って求めることができますが、ここではもう一度算出方法を振り返りながら求めること
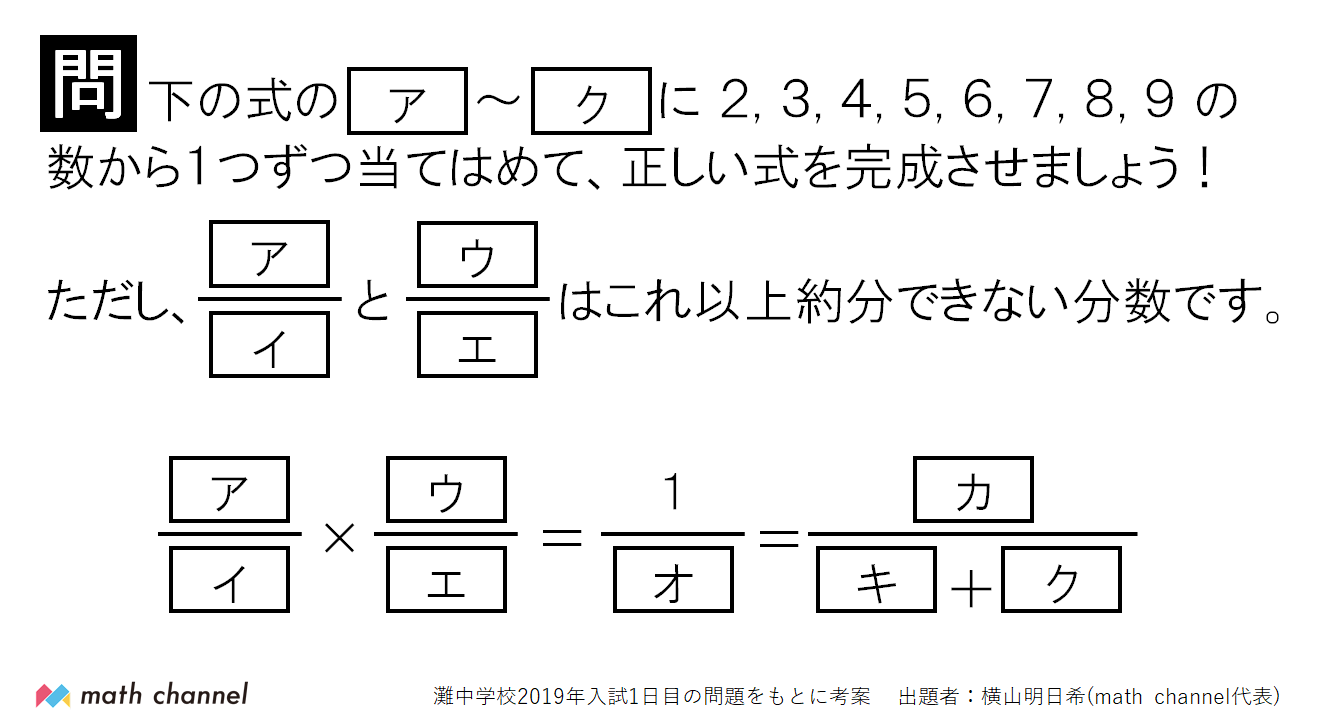
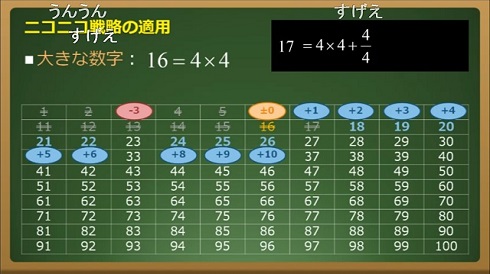
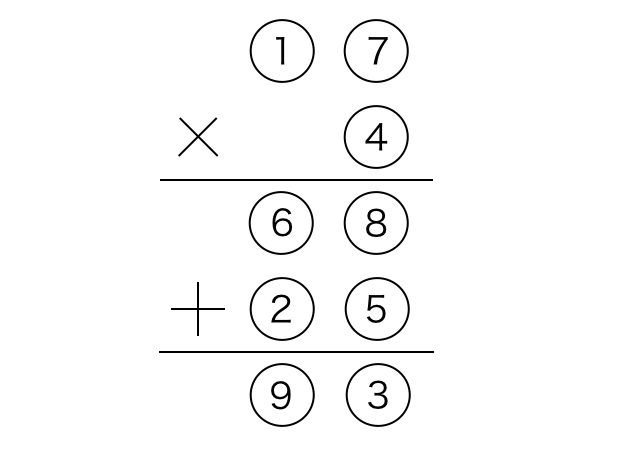
横山 明日希 1から9を1回ずつ使って式を完成させる問題 灘中の問題は左の式と真ん中の分数まで オまで だったけど これ 残った数字も使えるじゃん って気づいたので右の式も付け加えてみました こういう問題解けても楽しいし 作るのも楽しいです
1 から 9 の 数字 を 使っ て
1 から 9 の 数字 を 使っ て- google の CM で「1,1,5,8 で10を作る」が出題されていましたね♪答え と 一緒に 出来る子どもの数字イメージについて紹介したいと思います。子どもと一緒に解くときには、いきなり答えをいうのではなく、小出しに ヒントを出してあげてくださいね♪自分で解けると嬉しいですから♪ つまり、 正確な位置まで決めるような問題は順列 になり、 P P を使います。 C(組み合わせ)の問題の特徴 何かを選ぶ(だけ) 組み合わせを求めろと書いてある など つまり、 正確な位置は決めるわけではなく、選ぶだけのときは組み合わせ になり、 C C を使います。 難しい問題の場合は、直接的に「選びなさい」や「組み合わせを求めなさい」と書かれてい



数独のルールと解き方 Webニコリ
1つの数字が1回しか使えない場合 9c4 = (9*8*7*6) / (4*3*2*1) 1つの数字が繰り返し使える場合 9p4 = 9*9*9*92 days ago 海外「フロリダが緑のネオンカラーで輝くだろう」日本の研究者がダチョウの抗体を使って開発した、光るコロナウイルス検出マスクに、世界から興奮の声 コロナ, ニュース, 海 9 132人目の素数さん (月) id176opbwz 土、古、吉、西については 一松信が私的に使っていたものと一致するな。
計算フォーム 4つの数字を入力して、ボタンをクリックしてください。 警告数字が入力されていません。 1つ目の数字 2つ目の数字 3つ目の数字 4つ目の数字 計算して10をつくる 答え またこの3000個の数は各位が0~9までの10個の数が同じ回数ずつ登場する。 ゆえに3000÷10=300回 これをベースに考えていく (2) 19まで書いたときに1という数字は全部で何回書きましたか 解答 1000までに300+1 回(1000の分) 1999~00までに300+999回(00以外) 01~19まで 1から9の数字を1回ずつ使ってできる数の中で、一番小さい数は です。 ここから、上記 アルゴリズム を使用して、次に小さい数を求めます。 さらにそこから得られた数に対して上記 アルゴリズム を適用します。 これを繰り返すことによって順列を取り出すことができます。 手順の、 ② n i を桁小さい方からみていき、初めて n i < n i1 となる i を求めます ここで該当
難問 9ケタの数字 1〜9の数字をひとつずつ使った9桁の数字がある。 それを「abcdefghi」と表現する。 この時、 最初の1桁"a"は1で割り切れる; ある予備校の入塾テストで出た問題なのですが、解答が貰えず復習に困っています。 教えていただけないでしょうか。 (1) 0から9の数字を1回ずつ使って4桁の整数を作るとき、どの桁の数字を2つ選んで足しても9にならないような数はいくつできるか。サンプルプログラム 1から入力した自然数までの総和を それでは実際にfor文を使って、1から入力した自然数までの総和を計算するサンプルプログラムをみてみましょう。 入力した数値が自然数でない場合はif 〜 else文を使って、コメントを出力するようにしています。



こんな問題はいかがでしょう 数学 小学生の算数から数学の専門分野まで 会議室 サイエンスフォーラム
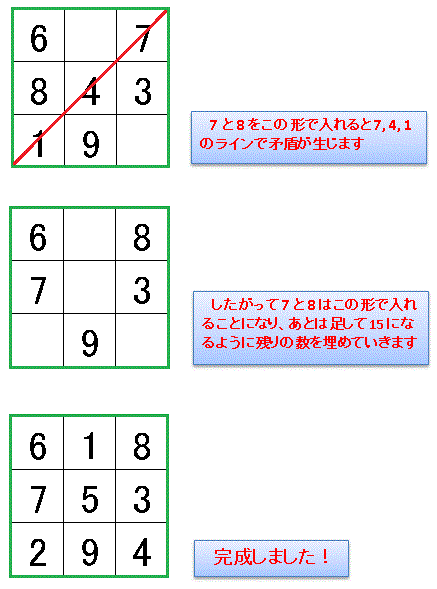



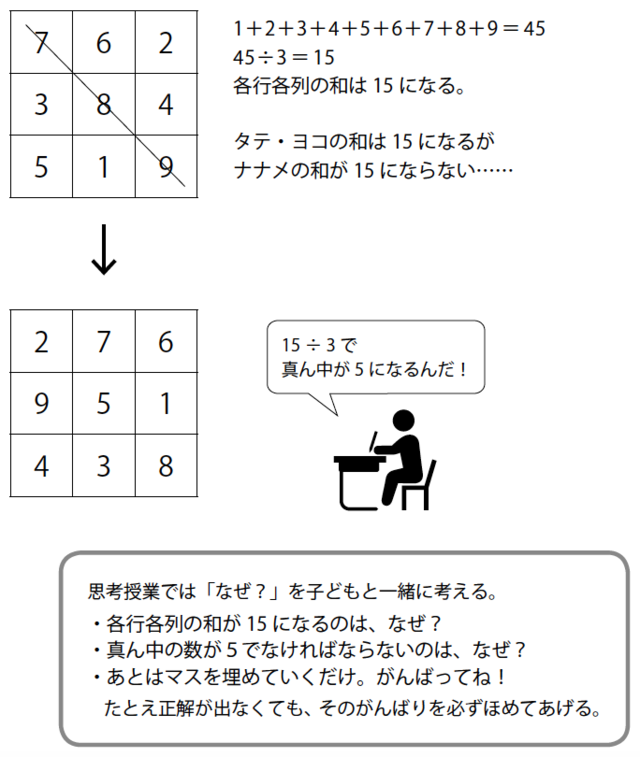
縦 横 斜め どのラインも足し合わせると15です Excel Vba 数学教室
数字の1から9を使って100を作る計算式( 2210) 新しい算数手品を思いつきました ( 1459) 特殊なサイコロを使った確率の問題 ( 0217)\((1,2,4,5)\) を使ってできる4桁の整数は、 千の位は4通り。 百の位は千の位で使った数以外の3通り。 十の位は千と百の位で使った数以外の2通り。 一の位は残った最後の数を入れるので1通り。 よって、\(4\times 3\times 2\times 1=24\) 個。 以上より、\(18\times 424=96\)個。(1) 家の人と数字カードを使って,バトルをしよう! 楽しみながら大きな数の学習ができるよ! ゲームを始める前に 下の数字カードを切り取って,0~9までの10枚のカードを2セット(2人分)作りましょう。 4年生算数 名前( )




0から9までの数字を1回ずつ使って りくのらひねもす囲碁ブログ
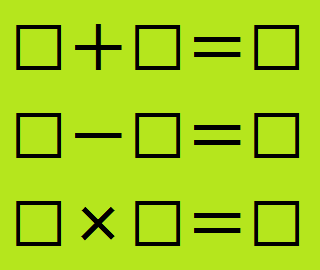



1 9の数字を入れて計算式を完成させよう
下の空欄を埋める問題です。 ただし、同じ数字は1回ずつしか使用出来ません。 × = × = 1週間解いてますが、分かりません。 どなたか数字に強い方、よろしくお願いいたします。m同じものを含む順列の問題です。 1、2、3、4、5、6を使って6桁の整数を作るとしたら答えは6!ですね? それを同じものの順列で割るのです。 偶数になるのは1の位が2ですから残りのを並べる順列を 同様に考えます。 場合の数の問題です。 0,1,2,3,4,5の5個の数字を全て使って整数を作るとき 5ケタの偶数は何通りあるか? 私の計算では1の位が0,2,4の3つで万の位に0が来ないから 3



小学生でも出来る算数クイズ その22 虫食い算 脳トレ 脳幹を64倍活性化




おもちゃ 無塗装 無垢材 1から9まで 数字を乗せた電車 丸文字タイプ おもちゃ 木のおもちゃ ラッピング方法
ここでは、数字を並びて整数がいくつできるかを数える、という問題を考えます。「場合の数」の分野ではよく出題される内容です。 3桁の整数はいくつできるか 例題1 (1) 9, 8, 7, 6, 5 の数字を使って3桁の整数を6x6は1~6の数字を、9x9は1~9の数字を、12x12は1~12の数字を一度ずつ、タテ、ヨコの列、(3x3のかわりに)ジグザグボックスに配置します。 Diagonal ナンプレ 9x9の盤面に与えられた数字をヒントに、1~9 の数字を埋めていきます。 1から9までの数字を1回だけ使って3桁の足し算の等式を完成させる すなわち、 = の の中に、1から9の数字が一つずつはいる。 まず、1から9までの数字は、奇数が5つ(1,3,5,7,9)、偶数が4つ(2,4,6,8)である。 そして奇数と偶数を足すと奇数に、奇数と




旧バージョン 4年算数 大きな数 8時間目 数字カードを使って 10けたの整数をつくりましょう Youtube



Iq問題 1から9までの数字を全て1回だけ使ってにしてください ネットカフェネットカフェ
ちなみにこの問題は高校生の頃解いたことがあるのですが、結論から言ってしまうと 「1〜9までの異なる4種類の数字の組み合わせで、10を作れないものは無い」 です。 さらに、一番難しい(方法が少ない)のは 「3 4 7 8」 の組み合わせです。 1~9までの数字を一回ずつ使って・・・。 質問します。 × = (4桁×1桁=4桁) の中に入る数字はすべて異なり、1~9までの数字を一回ずつ使用します。 この数式を満たす数字の組み合わせは何通りかあるそうです。 ちなみに、1963×4=7852という組み合わせは気合いで探しましたナンプレ 数字をヒントに1から9までの数字を埋めるパズルです 世界中で最も親しまれているパズルです。 楽しくて癖になる! ルールはとてもシンプルで簡単です。 語学も数学の知識も要りません。 幅広いロジックと難易度で楽しめます。 思考力・ロジカルシンキング力の向上に役立ちます。 ナン
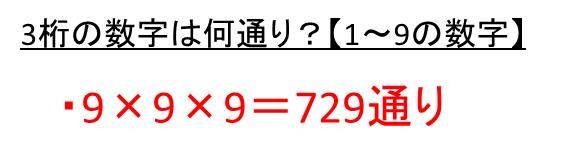



3桁の数字は何通りある 0 9や1 9の場合 5桁の数字は何通り パスワードやパスコードや暗証番号 ウルトラフリーダム



算数クイズ タテヨコ計算 脳トレ 脳幹を64倍活性化
25 Likes, 0 Comments 近江牛を使ったコース料理が味わえる肉処 牛慎 (@gyushin_niku) on Instagram "牛慎です! 年末年始の営業に関して、画像の通り営業致します! 新年も1日のお昼からオープンですので、ぜひご来店下さい😊 コースのみ前日までの予約制 それ以外はご予約不要です! 虫食い筆算で1から9までの数 (同じ数は一回しか使えない)で一番大きい数の答えになる数を当てはめ ベストアンサー:数字は9個までしか使えないので、 3けた+3けた=3けたになる計算でないと いけないことになります。 答えのけた数が変わらないので、 百の位では繰り上がりが起きな 1 /6/24 2300 数学 1〜9の数字を1回ずつ使って、筆算を完成させなさい概要 アメリカから日本行きの飛行機に乗った時に、 13時間というフライト時間をとっても持て余しました。 機内誌を見たところクイズが載っていたのですが、




再帰を使わない順列生成 1から9の数字を1回ずつ使ってできる数を 小さい方から順に列挙する アルゴリズム編 Javaエンジニア React Firebaseでアプリを作る
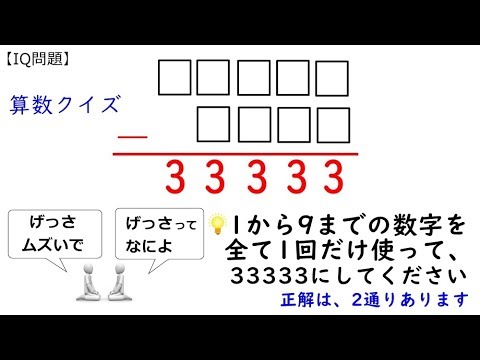



Iq問題 1から9までの数字を全て1回だけ使ってにしてください 算数クイズ 正解は100後に発表 Youtube
なので、一番左から二番目は\(2\)です。 と以下同様に考えていくと、すべての数字の数の条件を満たしていることがわかります。 その② 1,9,9,6を使って100と1000を作る 問題② \(1\), \(9\), \(9\), \(6\)の4つの数字を使い、\(100\)と\(1000\)となる計算式を作り 数学 1から9までの数字を一回ずつ使って ― =に なるようにするには、どの数字をどこにつかえばいいでしょうか? お教えくださいませ。 1 Likes, 0 Comments Ryoko (@ryoko611) on Instagram "' ビオレ クリアふきとりシート 花王株式会社からの提供でこちらをモニターしました。"




動画で解説 数秘超入門04 1から9までの数字のイメージ 数秘 占星術 タロット




4桁の数字は何通りある 0 9や1 9の場合 6桁の数字は何通り パスワードやパスコードや暗証番号 ウルトラフリーダム
全9桁"ABCDEFGHI"は9で割り切れる ということについて悩む必要はありません。 = 45 45は9で割り切れます。 つまり1〜9の数字をひとつずつ使った9桁の数字なら、 どのように順序を入れ替えても必ず9で割り切れます。 なので、最後の桁"I"は 応用例1:1~100までの数の合計を求める ループカウンタ変数を使って1~100までの数の合計を求めて表示してみます。 for文の条件を変更すれば1~1000でも、1~でも簡単に応用出来ることが分かります。 gokei_100c 1 面白くて不思議な数字の計算 – トップ 11 その① – 一年の日数である はやっぱり特別な数字? 12 その② – 二乗して足しても同じ数 13 その③ – 1~9の数字を一回ずつ使った分数の掛け算を成立させる 14



1から9の整数のうち 7つの数字を使う 直線で結ばれた3つの掛け算の答え Yahoo 知恵袋




0から9までの数字カードを使って スクールプレゼンター教材共有サイト スクプレ道場
1 その①:必ず自分自身に戻ってくる不思議な現象 2 その②:9を足された数が持つ性質 3 その③:9で割り切れるかはすぐにわかる 4 その④:どんな数字も大きい方から小さい方を引いた数は必ず9で割り切れる 5」 9を必ず3つ使って、1から9までの数字を作るというクイズをつくったので考えてみてください。 ルールとしては ・9は 必ず3回使用 する(9÷9=1だけど、これだけで1を作るのはNG) ・ 四則演算 、 カッコの使用 は OK ・ 分数 の使用は OK (記事内では、2分の3を3/2というように表記します) ・ 累乗 の使用は OK (記事内では、2の2乗を2^2というように表記します) ・ 根号 「√」の使用は



他の科目もグングン伸びるようになる 算数 の学び方とは 富裕層向け資産防衛メディア 幻冬舎ゴールドオンライン




1から9までの数字を一回ずつ使った3 3の行列のうち 固有値がすべて整数になる組み合わせ となりのぽぽろ
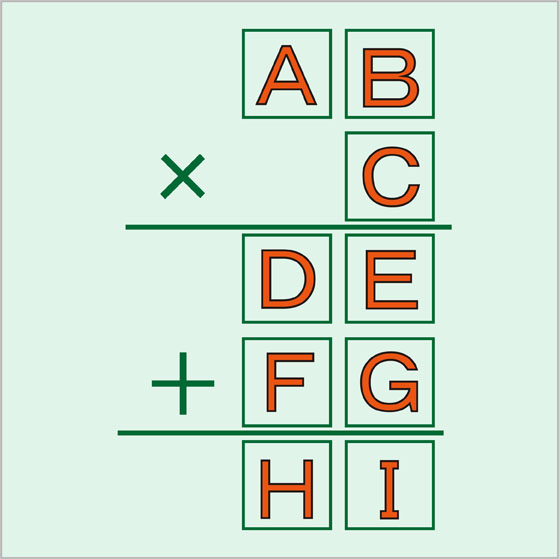



1 9までの数字を に入れて正しい式にせよ この問題 根気強さが必要 秒刊sunday




和からの日常 ミステリー編 美しい数 数学 統計教室の和から株式会社
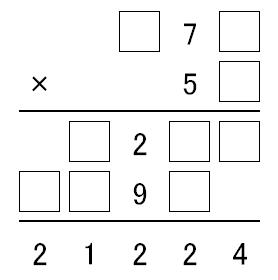



数学クイズ 9 あなたの脳を256倍活性化 楽天ブログ




確率です 解説見ても分からなかったんで教えて下さーーーい Clearnote




縦 横 斜め どれを足しても同じ数 不思議なパズル魔方陣 ふむふむセレクト 小学生向け 新潟日報教育モア



超難問パズル これが解けたらiq140 Send More Money お金もっと送って パズル系 Beauty Healthy




算数パズル 意外と解けない魔方陣の基本問題 理論的に解きましょう Youtube
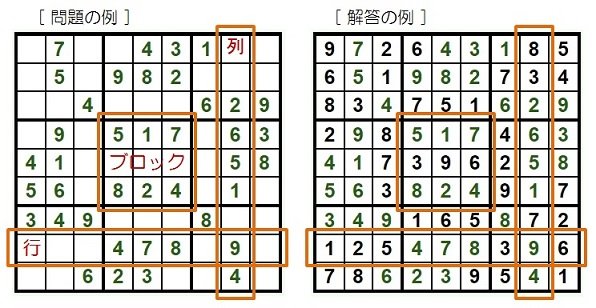



ナンプレ85のルールと特徴



3333になるように1 9までの数字を1回ずつ使って筆算 Yahoo 知恵袋



Chiyoda Cosw Or Jp




脳を活性化させる足し算パズル サムクロス 集中力 暗算力がぐんぐんアップ ギャレス ムーア Moore Gareth 本 通販 Amazon



1から9の数字を1回ずつ使って100になる足し算を教えてください お願いします Yahoo 知恵袋



面白クイズ 分かると簡単 1 から 9 の2桁の数字の平均を計算する
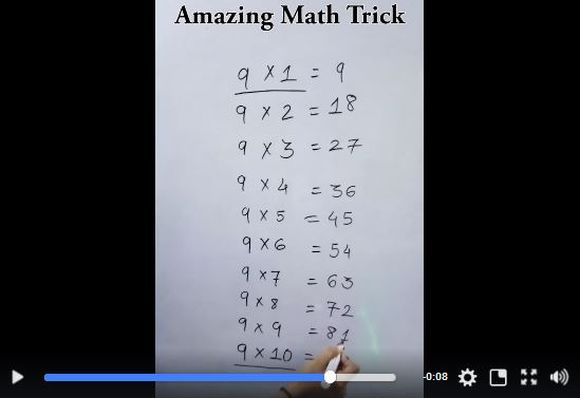



知ってた 九九の9の段 に隠された驚くべき秘密 ロケットニュース24
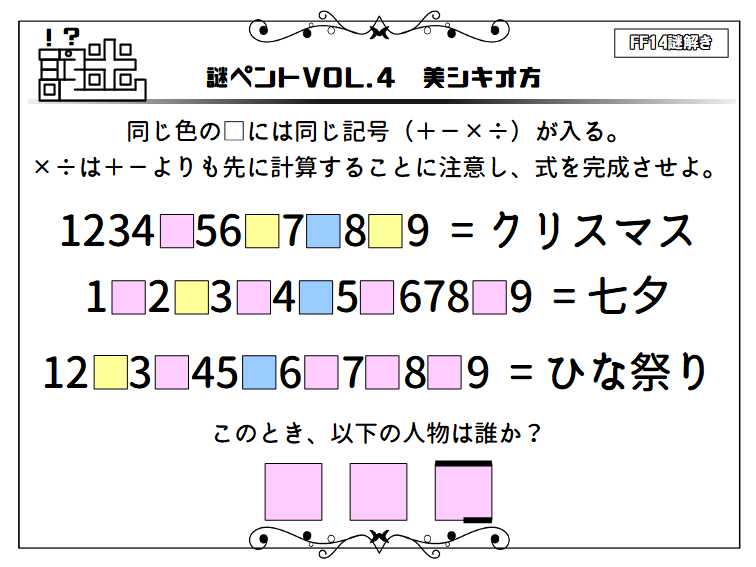



Pipins Fortress Blog Entry 謎ペントvol 4 美シキオ方 と Vol 3の解説 Final Fantasy Xiv The Lodestone



1から9までの9個の数字をすべて1回ずつ使って9桁の整数を作 Yahoo 知恵袋
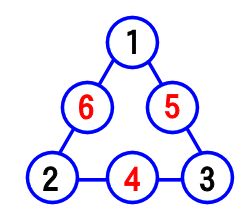



三角形の方陣算 一辺3
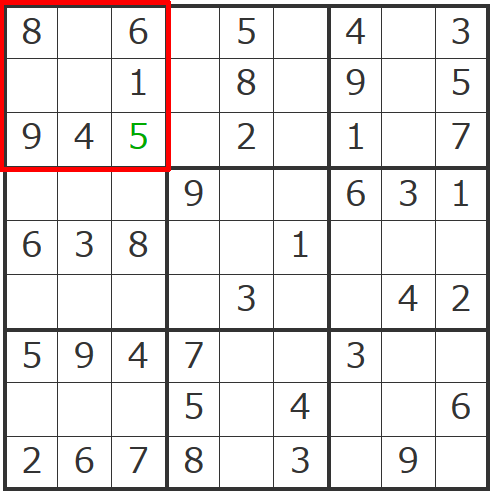



ナンプレの基本テクニック2 ナンプレ7



この四角に1 9までの数字をうめて完成させてください 同じ数 Yahoo 知恵袋



魔方陣の問題です 右の図のようなマス目の中に1から9までの数字が1つずつ入って Yahoo 知恵袋
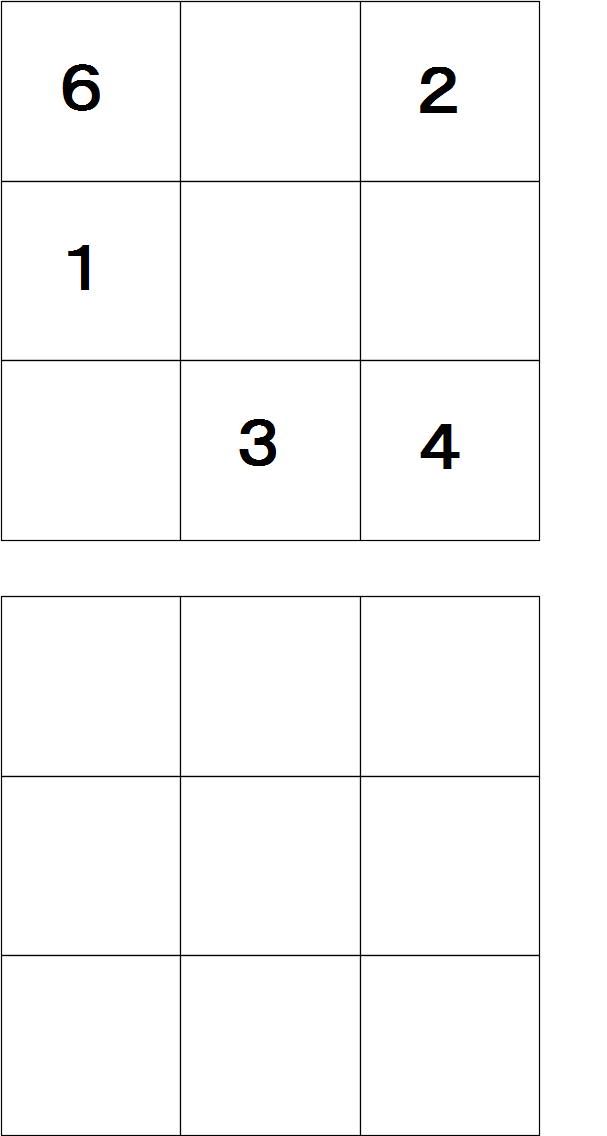



魔法陣 御三家中学受験 桜蔭 開成 東大サピックス家庭教師 ファインウェブ 楽天ブログ
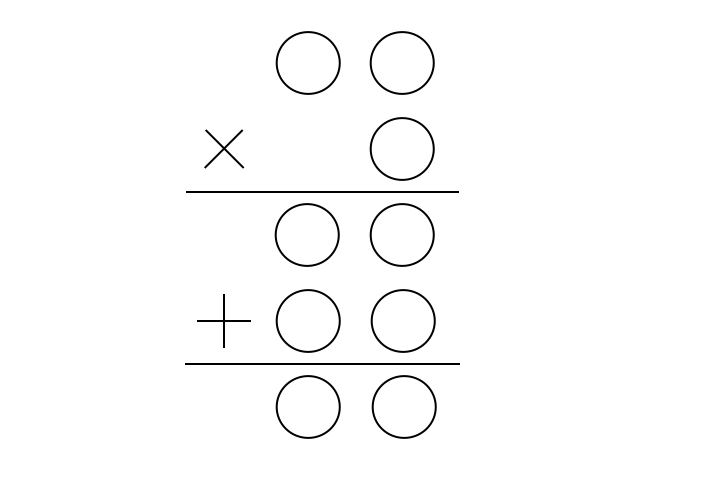



ひらめき 脳トレ問題 計算 図形編 回答編 家族や友達とチャレンジ
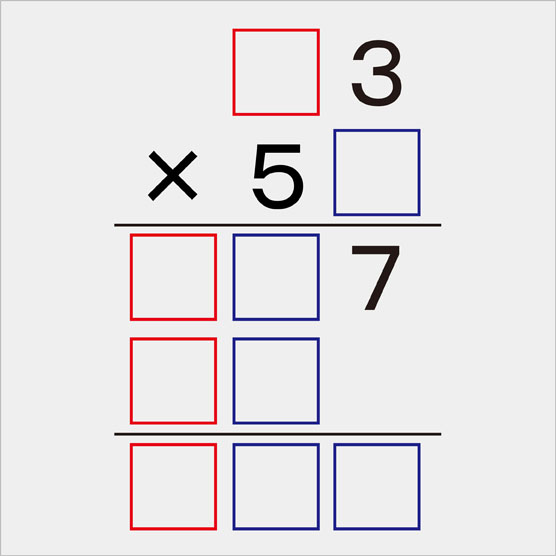



空欄に当てはまる1桁の数字を答えよ 赤い空欄に0は入れてはいけない 秒刊sunday
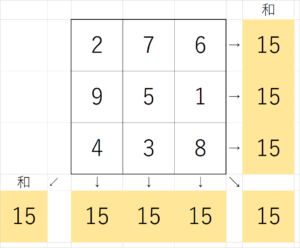



積の魔方陣 Fukusukeの数学めも




カッコ1番はわかったのですが カッコ2から分かりません 答えは組み合わせ Clearnote




動画で解説 数秘超入門04 1から9までの数字のイメージ 数秘 占星術 タロット




1 から 9 までの数字を使って引き算の式を完成させるには 1 から 9 数学 教えて Goo



4つの4 で1 100までの数字を作ろう 数学パズルを解説する動画が親切に解き方をおしえてくれる ねとらぼ




算数ジャンプ問題 たし算の筆算 授業力アップ 学級経営の話



ガスコン研究所



1から10までの数字のうち 英語にもあるものってなー



2
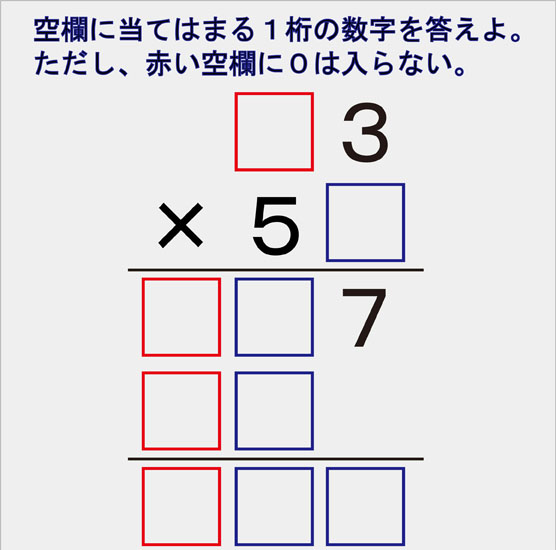



空欄に当てはまる1桁の数字を答えよ 赤い空欄に0は入れてはいけない 秒刊sunday




カラフルなかわいい落書き怪獣ベクトル数値セット1 から 9 までの数字かわいいをベクトルしますフラット スタイル デザイン漫画数値のセット数字 のカウントや数学を学ぶ子供のためのコレクションです算数を勉強している子供の野生モンスター アルファベットのベクター



1
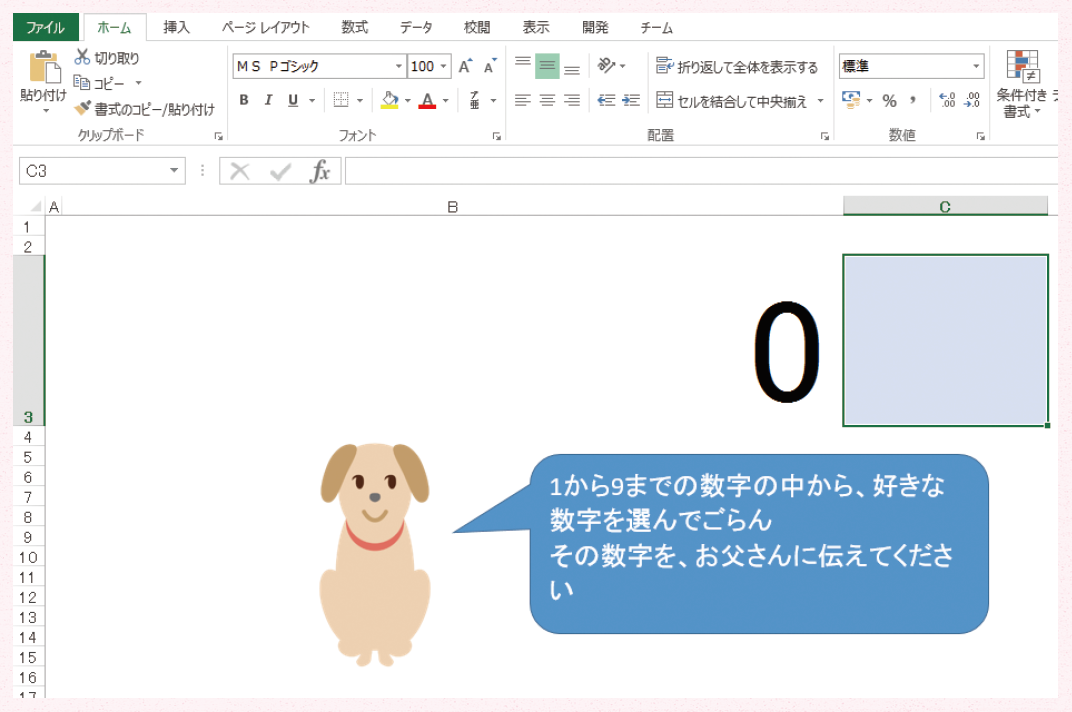



数 の不思議はオートsumとお父さんが教えてくれた エクセル親子ゲームで学ぶ コンピュータっぽい考え方 4 1 3 ページ It




数aの順列です 1 8 Clearnote




数独のルールと解き方 Webニコリ




ニコニコhappy Life 数学クイズ Facebook




吉田博士のパズル学校 18 問題編 中日新聞しずおかweb




マスに入る数字は何 すき がみつかる 放課後たのしーと




9は不思議な数字 五つの9の数学的な性質について詳しく紹介 数学の面白いこと 役に立つことをまとめたサイト
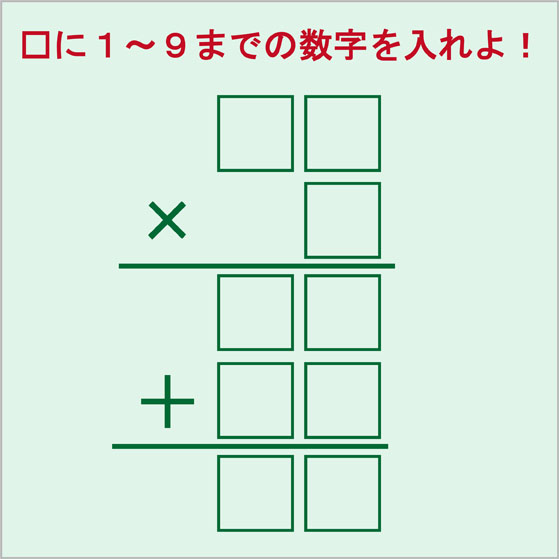



1 9までの数字を に入れて正しい式にせよ この問題 根気強さが必要 秒刊sunday



ひらめき 脳トレ問題 計算 図形編 回答編 家族や友達とチャレンジ



ダウンロード済み 1 から 9 の 数字 を 使っ て ドラえもんの壁紙
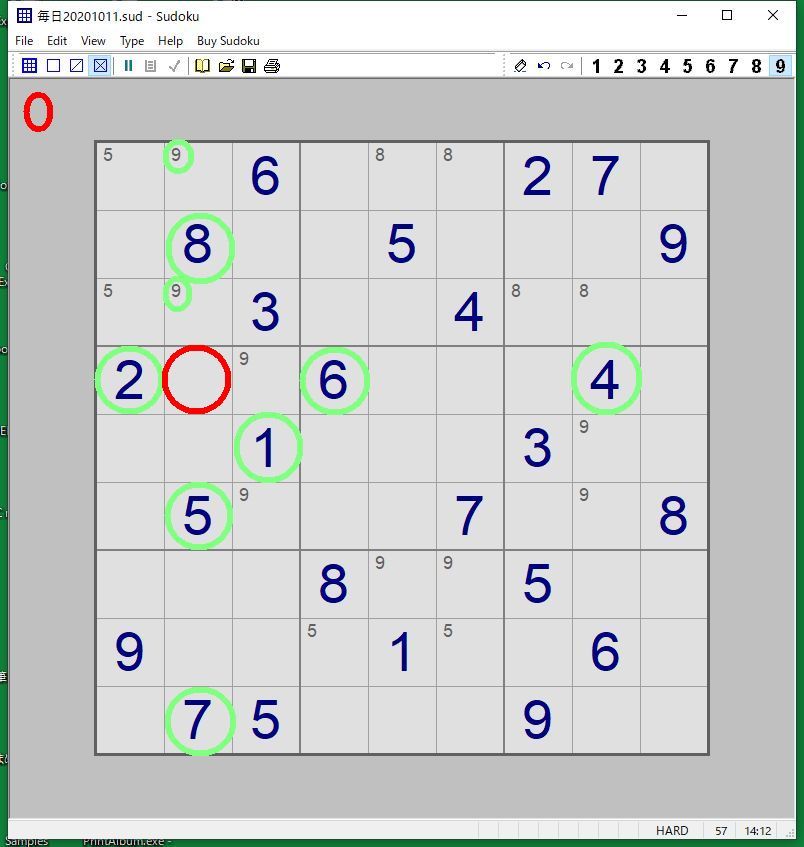



辛口数独 毎日新聞10月11日付朝刊 の解き方のヒント 大道無門 パソコンとインターネット 楽天ブログ




覆面算 1から9の数字 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください




旧バージョン 4年算数 大きな数 8時間目 数字カードを使って 10けたの整数をつくりましょう Youtube




数秘術からみえる 生まれながらに持っているマイナンバーとは
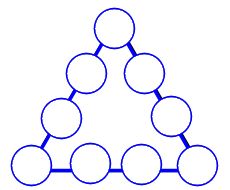



三角形の方陣算 一辺4




0から9までの10種の数字を使い 4つの数字を並べて4桁の整数をつくる Clearnote




ピーターからの問題 1から9までを使って分数の穴埋め算 解答のjavascriptプログラム Javaエンジニア React Firebaseでアプリを作る



1 9までの整数を1回ずつ全て使って以下の式が正しく成り立つように Yahoo 知恵袋




横山 明日希 1から9を1回ずつ使って式を完成させる問題 灘中の問題は左の式と真ん中の分数まで オまで だったけど これ 残った数字も使えるじゃん って気づいたので右の式も付け加えてみました こういう問題解けても楽しいし 作るのも楽しいです



9マス計算パズル 自由気ままに Go 楽天ブログ




分数に1 9までの数を1回だけ入れて 1にする問題 画像の の中に1から 数学 教えて Goo



Kadai33a
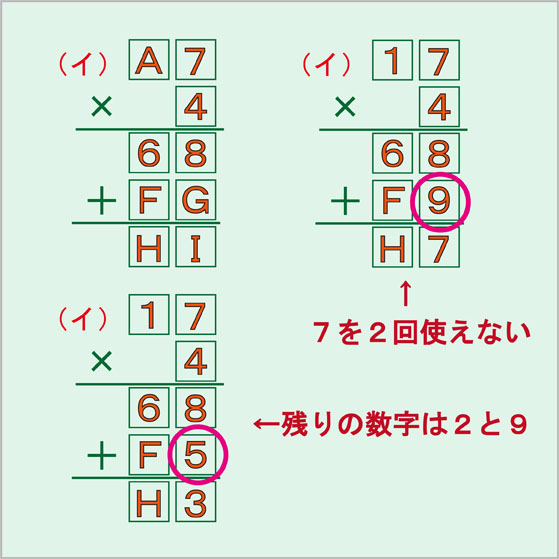



1 9までの数字を に入れて正しい式にせよ この問題 根気強さが必要 秒刊sunday
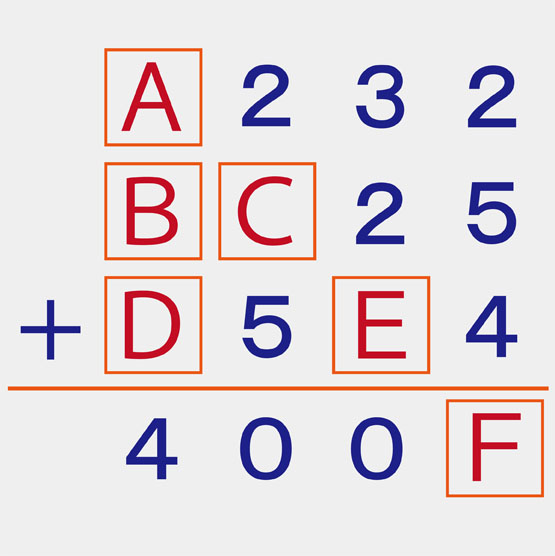



論理的な思考ができる人はすぐに解けるらしい 消えた数字を見つけて元の式を復元せよ 秒刊sunday




数字 9 の掛け算の答えが持つ不思議な性質 9はマジックナンバー 数学の面白いこと 役に立つことをまとめたサイト



1から10の中で数字を選んでと言ったとき 一番選ばれない数字は何番ですか Quora




電卓を使った面白い遊び 数学トリック 数学の面白いこと 役に立つことをまとめたサイト




急いでます 教えてください お願いします 答えだけでも Clearnote
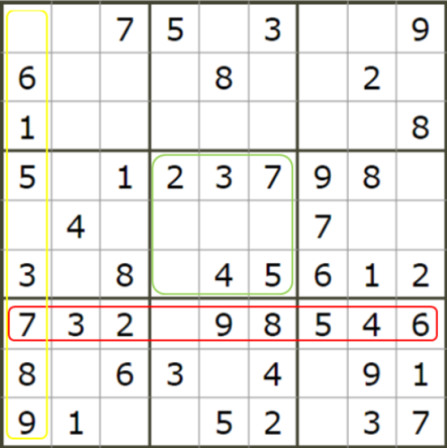



一押しインターネット Npo法人シニアネットクラブ 日野教室のブログ



かけ算の筆算 Zattaなプログラム




4年算数 大きな数8時間目 数字カードを使って 10けたの整数を作りましょう Youtube



1から9の数字を使って100になる足し算を教えてください お願 Yahoo 知恵袋
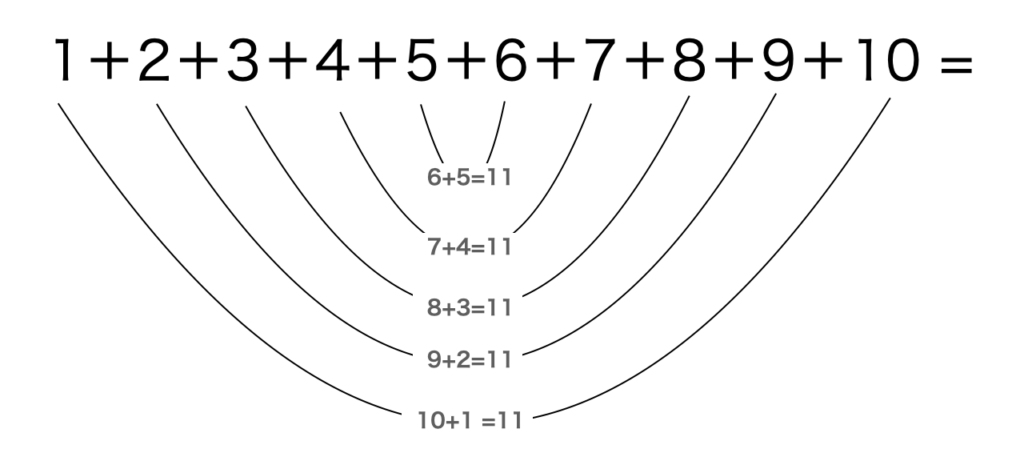



1から10までの数字を足す問題 簡単 瞬時に計算する方法をご紹介




確率の問題です 全て 解き方がわかりません Clearnote




高校数学a 大小関係が決められた数字の順列 差の条件がある選び方 受験の月



1から9までの数字を1回だけ使って3桁の足し算の等式を完成させる 倒錯の森 はてな




思い浮かべた数字を即 当てます 数学マジック の奥深き世界 横山 明日希 ブルーバックス 講談社 2 3



1から9までの数字で一番かっこいい数字はどれだと思いますか Quora




算数 数字カードの活用法 3桁のたし算 授業力アップ 学級経営の話



1から9の数字を1回ずつ使って100になる足し算を教えてください お願いします Yahoo 知恵袋




数字のパズルゲーム いろいろな数字を使ったパズルゲームの紹介 数学の面白いこと 役に立つことをまとめたサイト




マスに 3 11 全ての数字を入れ合計を同じにする問題 解けたら天才 秒刊sunday




数字のパズルゲーム いろいろな数字を使ったパズルゲームの紹介 数学の面白いこと 役に立つことをまとめたサイト




あなたは何番の数字を選びましたか ふまふまふーまとサクッと日常
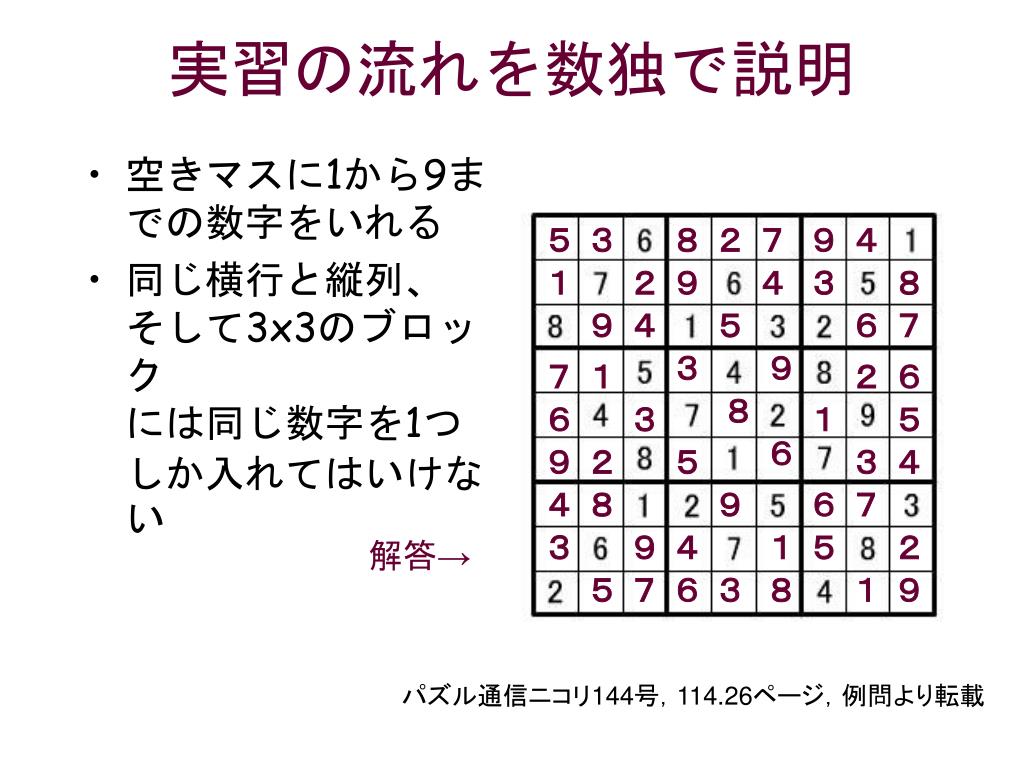



Ppt 整数計画法によるパズル解法 実習報告 Powerpoint Presentation Id



1




ビット 十進数と二進数 十進数 0から9までの数字を使って 0 1 2 3 4 5 6 7 8 9 10 11 12 と数える 二進数 0と 1を使って 0 1 10 11 100 101 11 0 111 と数える Ppt Download
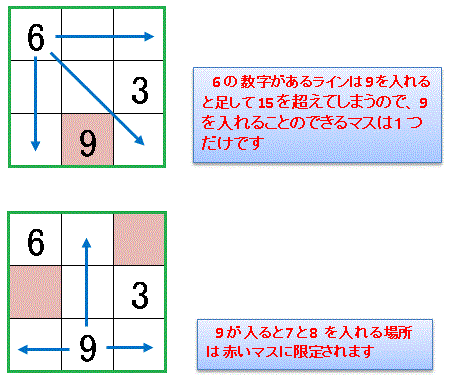



縦 横 斜め どのラインも足し合わせると15です Excel Vba 数学教室
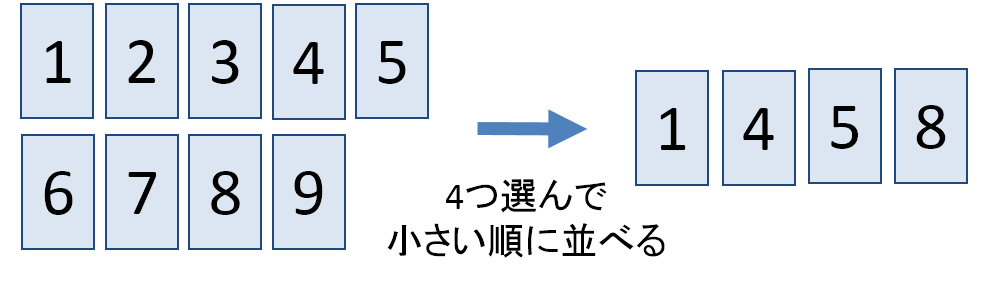



7 3 Cの使い方 統計学の時間 統計web



0 件のコメント:
コメントを投稿